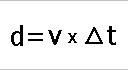|
1-La géométrie du système |
|---|
|
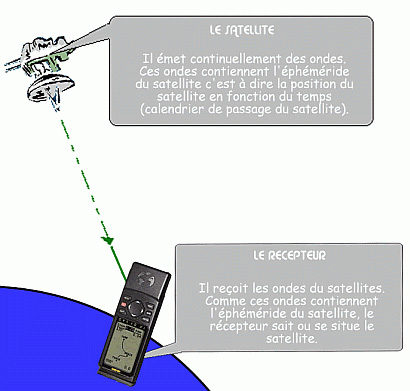
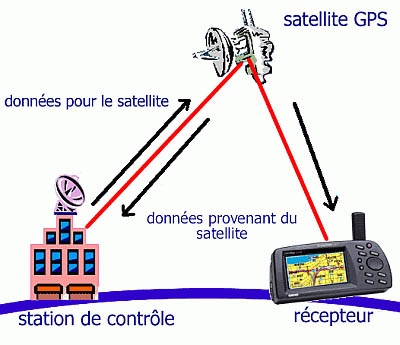
Le segment spatial se compose de 24 satellites formant la constellation GPS. Sur ces 24 satellites 21 sont opérationnels pour servir au système de positionnement par satellites. · La communication vers les récepteurs est dite unidirectionnelle ou descendante (seulement du satellite vers le récepteur). · La communication vers les stations de contrôle est dite bidirectionnelle ou ascendante - descendante (du satellite vers le récepteur et vice versa). Ces satellites émettent en permanence deux ondes appelées L1 et L2. Ces ondes contiennent des informations à destinations des récepteurs et qui sont:
Le segment de contrôle se compose des cinq stations qui surveillent en permanence l'activité des satellites du système GPS/NAVSTAR. Les
stations de contrôle et les satellites communiquent ensemble et
permettent ainsi des corrections d'horloge, de trajectoire. La
station de contrôle principale de Colorado Springs envoi les
éphémérides au satellites de la constellation
G.P.S. Les satellites envoient continuellement des ondes contenant toutes les informations nécessaires au récepteur GPS pour calculer sa position: comment le récepteur utilise t-il ces informations?
|
|
2- Principes de fonctionnement |
|
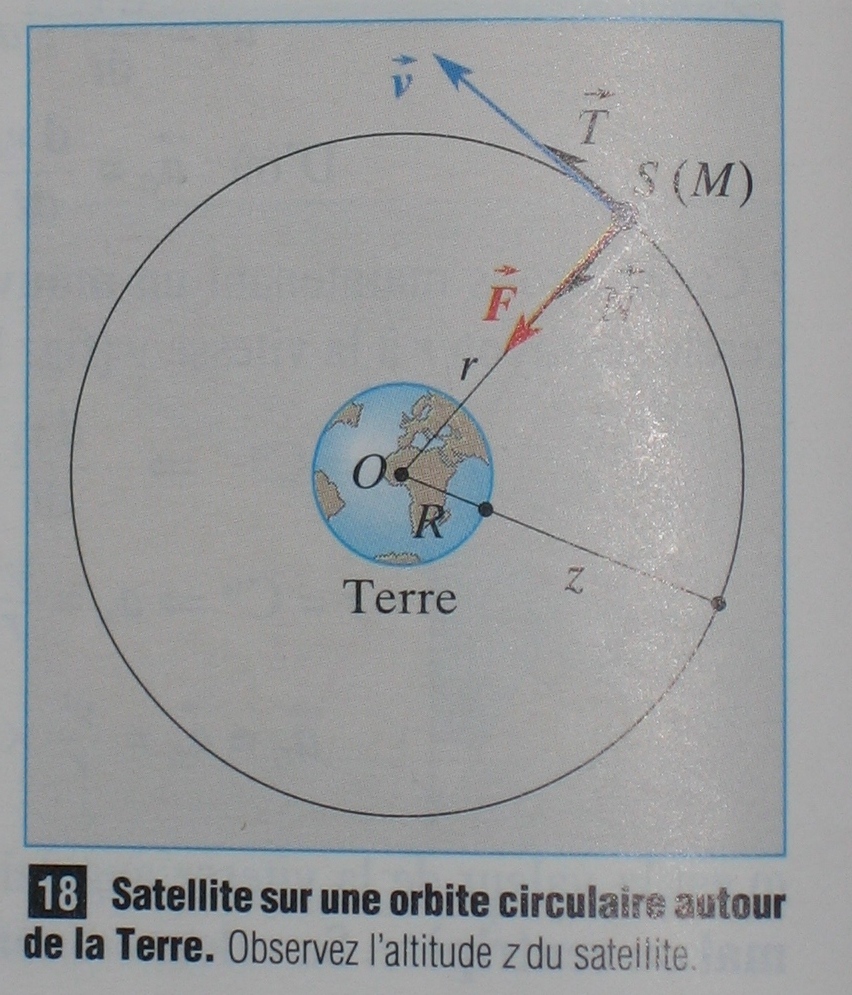
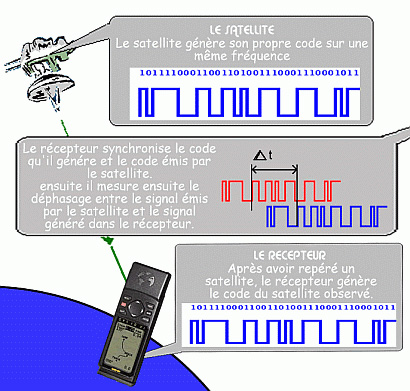
A- Le calcul de la distance Dans la démarche visant à trouver la position d'un point sur la terre grâce au système GPS, la première étape et le calcul de la distance.
Par ailleurs, on sait que les ondes voyagent à la vitesse de la lumière (en théorie)
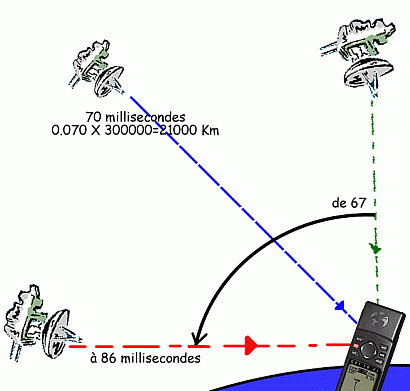
Un mot sur la précision des horloges: A la
vitesse de la lumière les 20 000 kilomètres qui nous
séparent des satellites sont franchis en 0,007 à 0,008
seconde. Pour être précis, la durée du trajet de
l’onde peut varier de 67 à 86 millisecondes selon que le
satellite se trouve pile au dessus du récepteur ou presque à
l’horizon.
Exemple:
B-La triangulation: Nous venons de voir comment avoir la position du satellite et la distance récepteur satellite mais cela ne nous donne pas la position du récepteur.
On a pour trouver la position de l'utilisateur une équation à 3 inconnues : X, Y, Z, Pour résoudre une équation à 3 inconnues, il est nécessaire d'avoir au moins 3 satellites qui donneront chacun une partie de la solution. Regardons
ce qui se passe avec 2 satellites :
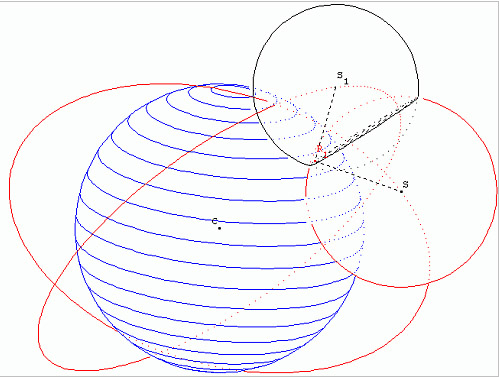
Ici on voit que l'intersection de 2 sphères est un cercle. Le récepteur se trouve sur ce cercle.
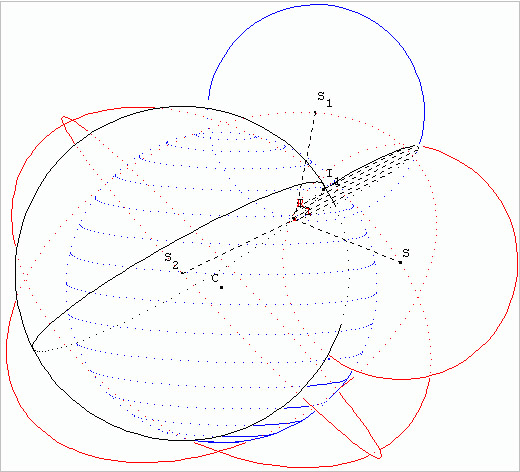
On remarque que l'intersection du cercle (issue de l'intersection des deux premières sphères) avec la troisième sphère forme deux points (I1 et I2) dont l'un sur la figure est confondu avec la position du récepteur donc, on a trouvé la position du récepteur. Cependant l'autre point à une position invraisemblable.
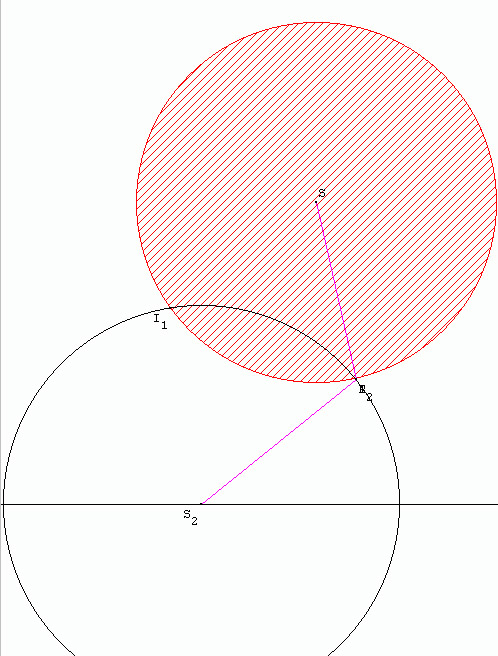
On peut aussi regarder cette dernière étape dans le plan.
Dan cette figure Le cercle rouge hachuré représente l'intersection des deux premières sphères. Le cercle noir représente la section de la troisième sphère qui va couper le premier cercle rouge. Le point I2 est confondue avec le point correspondant au récepteur. Le point I2 répresente la position exacte alors que le point I1 est faux. En résumé, la triangulation consiste à trouver le point d'intersection de trois sphères en sachant que:
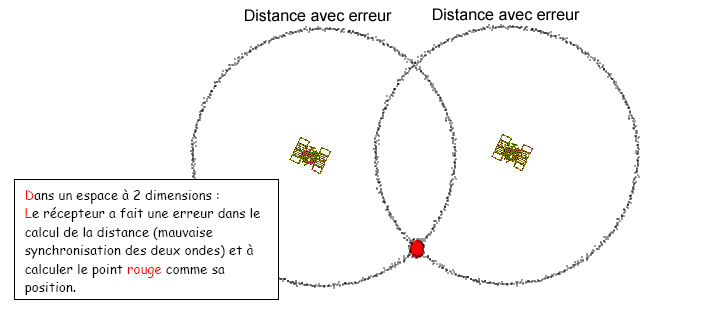
Utilité d'un quatrième satellite Un quatrième satellite peut être utilisé par le récepteur pour corriger les défaillances de sont horloges lors de la synchronisation des signaux (calcul de la distance). Pour observer l'utilité d'un quatrième satellite raisonnons dans un espace à deux dimensions.
Dans le plan (espace sans l'altitude): 2 dimensions donc 2 satellites + le 3ème pour corriger les erreurs de temps.
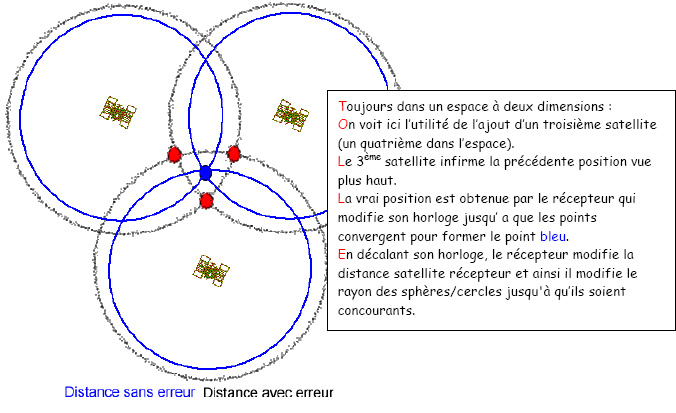
Maintenant avec un troisième satellite (un quatrième dans l'espace).
Dans l'espace la situation est identique a celle du plan avec un satellite supplémentaire pour l'altitude. Donc le satellite supplémentaire est le 4ème.
C: Le calcul des coordonées
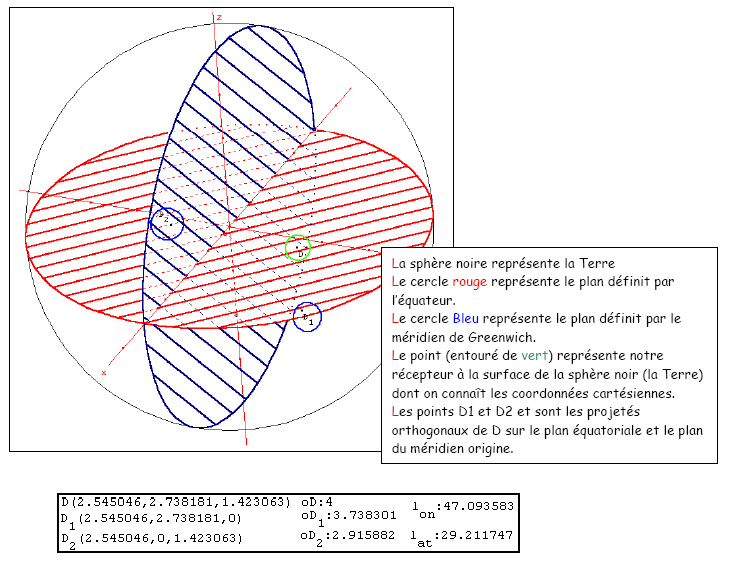
Les coordonnées polaires : Le récepteur connaît les coordonnées cartésienne, donc on souhaite avoir les coordonnées polaires c'est à dire la latitude et la longitude.
Conclusion Le récepteur grâce aux signaux envoyés par les satellites a réussi à trouver sa position.
Enfin Il calcule et trouve ses coordonnées cartésiennes puis les convertis en coordonnées polaires.
|
|
|





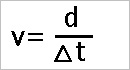 puis
puis